[最も好ましい] 平行四辺形とは 144104-平行四辺形とは

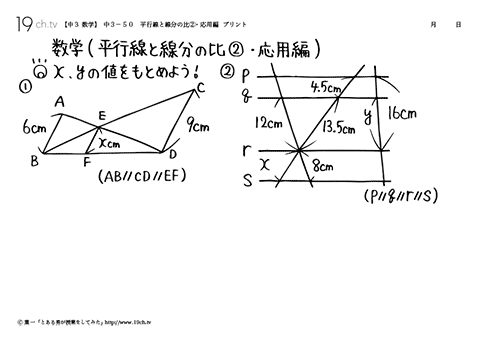
主な違い： 台形は四辺形で、平行な辺が少なくとも1対あります。 この図は台形と呼ばれています。 平行四辺形は、2対の平行な辺を持つ四辺形です。 台形と平行四辺形という言葉は、一般に数学と幾何学で見られます。 これらの用語は、角度を学び理解するために一般的に使用されているしかし，ここに一つ問題が生じる。 ベクトル (a 11, a 12) と (a 21, a 22) が張る平行四辺形の面積は，ベクトル (a 21, a 22) と (a 11, a 12) が張る平行四辺形の面積を表すところの と同じであり，そして上の定義に従えば，つぎのようになる：ここではベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しいということについて説明します。 以前の説明 ではベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が張る平行四辺形に、 そっと \(\ \overrightarrow{a} \times \overrightarrow{b}\\) と書いていました。

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

平行四辺形とは

[最も共有された！ √] 平行線と線分の比 三角形 546944-平行線と線分の比 三角形

三角形の1辺に平行な直線で他の2辺を切り取るときの線分の比 2つの直線を平行な直線で切り取るときの線分の比 〇三角形の角の二等分線と線分の比 三角形の2辺を等しい比に切り取るときの線分の位置関係 小学生・中学生が勉強するならスクールTV。全国の学校の教科書に対応した動画で学習三角形の合同条件 平行線と線分の比 証明のしくみ 中点連結定理 5章 平面図形（中1学年） 対称な図形 垂線の作図 線分の垂直二等分線 角の二等分線 章 相似と比（中3学年） 似比 三角形の相似条件と証明 小4学年～6学年 5章 三角形と四角形（中2学年）平行線と線分の比 平行線と線分の比 1 pq//bc ⇔ apab = aqac 2 pq//bc ⇔ appb = aqqc 3 pq//bc ⇒ apab = pqbc a p q p q a b c b c ※3だけ逆は成り立たない。 角の二等分線と比 角の二等分線と比 1 abcの∠aの二等分線と辺bcとの 交点pは辺bcをabbcに内分する。

中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch

平行線と線分の比 三角形

選択した画像 四角形 イラ���ト 265610-図形 四角形 イラスト

いろいろな図形のイラスト かわいいフリー素材集 いらすとや

四角形とドットの幾何学的背景 正方形点のイラスト素材／クリップアート素材／マンガ素材／アイコン素材 四角形とドットの幾何学的背景 正方形とドットの幾何学的背景、ベクトルイラスト。Let canvas_height = 400;

図形 四角形 イラスト

分数 わり算 127832-分数 割り算 計算機

分数のわり算文章題2 目標時間 NO2 名前 ／5点 1 ℓ の 9 は 5 ℓ 5 4 180kgは kgの3 3 5 2 45 63 3 1mの重さが2 kgの金属の棒が 5 mあります。 この棒を11 7 4 面積が15 1 ㎠横が5 2 ㎝の平行四辺形の高さは何cmですか。 3 317分数のわり算の練習 もっと練習 まとめて印刷 分数のわり算 基本（問題） 分数のわり算 基本（解答） Tweet; 分数の割り算 ⇒ 逆数にして掛ける これが自動的にできるようになれば、それでokです。 4 計算途中で約分してもok おさらい①、おさらい②も含めて、ここまでで、分数の足し算、引き算、掛け算、割り算と一通りの計算方法を学んできました。 ここでは、分数の計算をちょっとだけ簡単

分数と小数の混じったかけ算 割り算 Youtube

分数 割り算 計算機