三角形の1辺に平行な直線で他の2辺を切り取るときの線分の比 2つの直線を平行な直線で切り取るときの線分の比 〇三角形の角の二等分線と線分の比 三角形の2辺を等しい比に切り取るときの線分の位置関係 小学生・中学生が勉強するならスクールTV。全国の学校の教科書に対応した動画で学習三角形の合同条件 平行線と線分の比 証明のしくみ 中点連結定理 5章 平面図形(中1学年) 対称な図形 垂線の作図 線分の垂直二等分線 角の二等分線 章 相似と比(中3学年) 似比 三角形の相似条件と証明 小4学年~6学年 5章 三角形と四角形(中2学年)平行線と線分の比 平行線と線分の比 1 pq//bc ⇔ apab = aqac 2 pq//bc ⇔ appb = aqqc 3 pq//bc ⇒ apab = pqbc a p q p q a b c b c ※3だけ逆は成り立たない。 角の二等分線と比 角の二等分線と比 1 abcの∠aの二等分線と辺bcとの 交点pは辺bcをabbcに内分する。
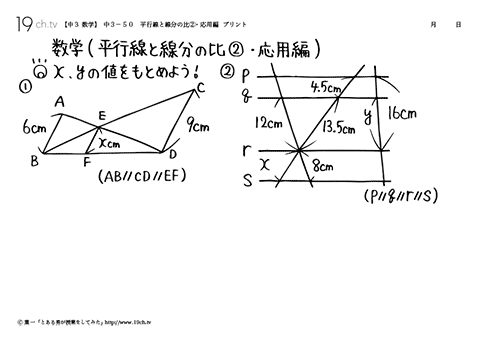
中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch
平行線と線分の比 三角形
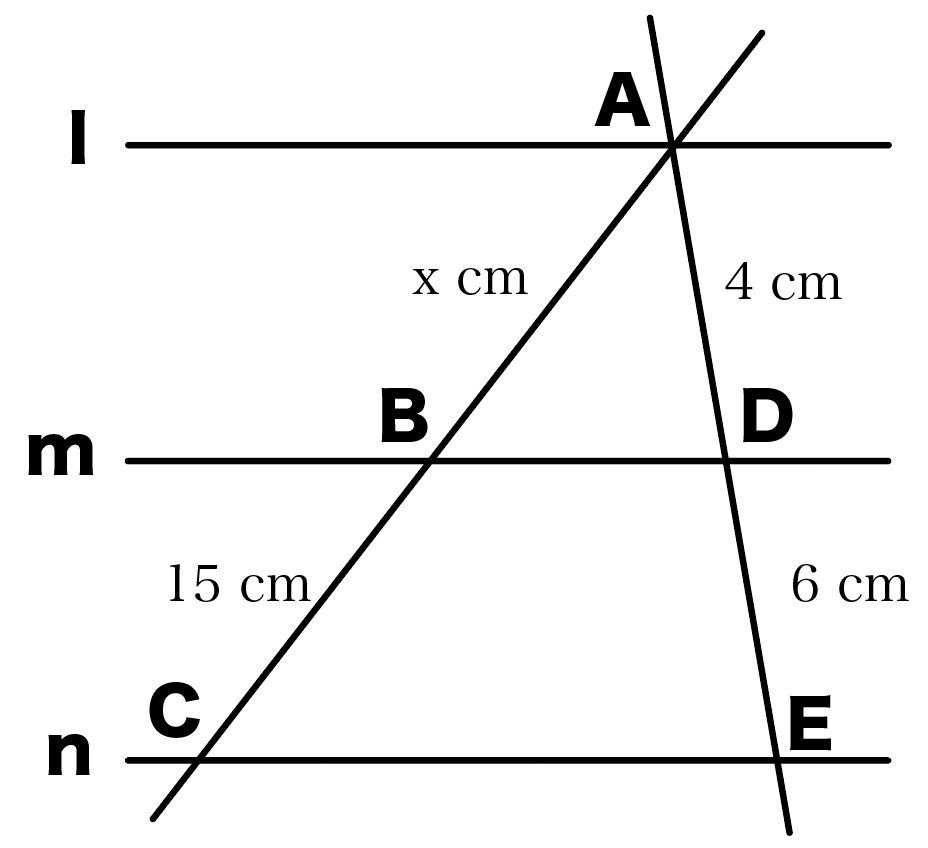
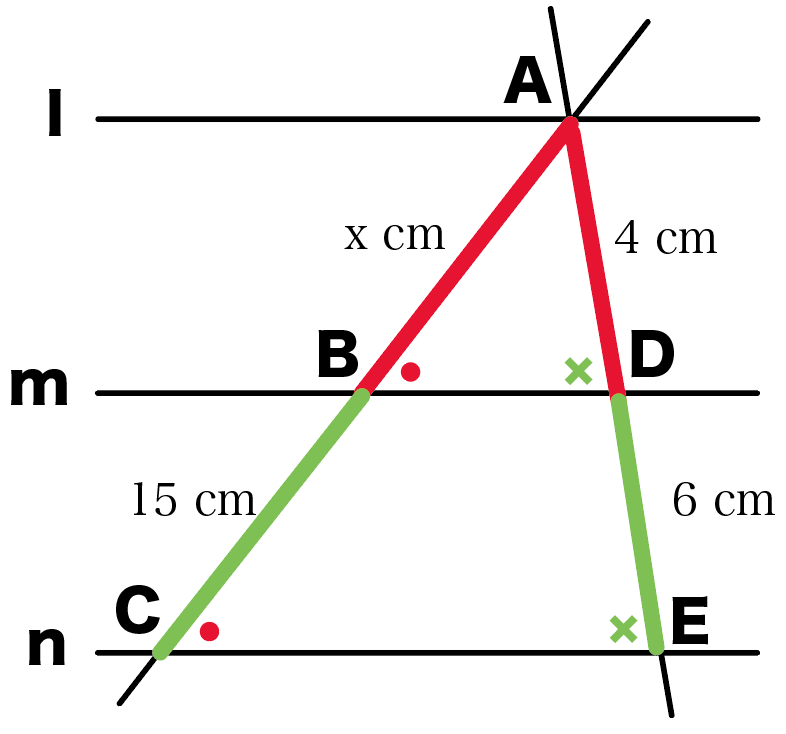
平行線と線分の比 三角形-平行線 と 線分 の 比 の 性質 を , 平行 線 の 性質 や 三角形 の 相似 を 基 に 考 察 し , 証明 することができる 。 平行線と線分の比の性質を 用いて,線分の長さや比を求 めることができる。 平行線と線分の比の 性質を理解すること ができる。平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. bd//ce のとき まず




中学3年数学練習問題 図形と相似 平行線と線分の比の問題
(3)三角形の相似条件や平行線の線分の比に関する性質などを使って、性質を証明することができ、問題 解決に活用する。(数学的な技能) (4)相似に関する用語・記号、三角形の相似条件や平行線と線分の比に関する性質などを証明することが できる。平行線と線分の比1 名前 下の三角形と線分の比についての定理について次の( ) をうめなさい。 相似な図形 平行線と線分の比11・補助線5は,三角形の相似と平行線の性質を使う。これだけは, 三角形の比の定理を使わなくても証明できる。 ・補助線6は,どうやっていいかよく分からない。 ・相似な三角形を利用するためには,平行線が大切だけど,今回の
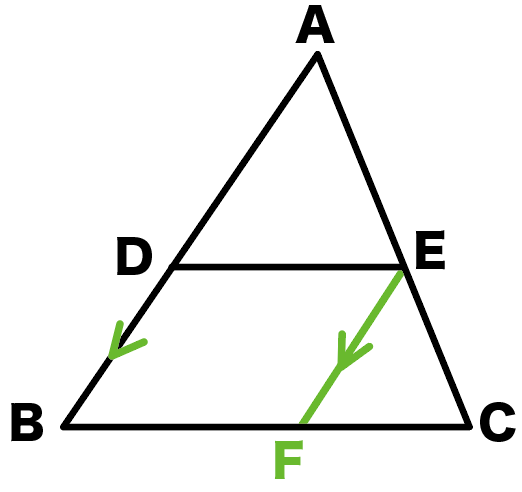
About this project 本サイトは、全国約12万6千人(16年時点) の不登校などで個別指導を必要とする子どもたちや、全国約3万4千人(16年時点) の日本語指導を必要とする外国人の子どもたちのために、 多言語に対応した数学学習コンテンツです。 いつでも、どこでも、どの段階からでも、 3分間三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。 となっている。 となっているんだ。 平行線によって・平行線と線分の比についての性質を,平行線の性質や三角形の相似条件を用いて証明 することができる。 ・相似な図形の相似比と面積比及び体積比を調べ,文字式を用いるなどしてそれらの関 係について考えることができる。 (思考・判断・表現)
平行線と線分の比とはこんなやつだね。 ⇒ 相似平行線と比の利用、辺の長さを求める方法をまとめて問題解説! 三角形の外角の二等分線と比 \( abc\)の\(∠a\)の外角の二等分線と辺\(bc\)の延長との交点は辺\(bc\)を\(abac\)に外分する。質、三角形の相似 条件などを、数学 の用語や記号を 用いて簡潔に表 現したりする技 能を身に付けて いる。 相似の意味、三角形 の相似条件、平行線 と線分の比について の性質、相似比と面 積比及び体積比の関 係などを理解し、知 識を身に付けてい る。平行線と線分の比 1 三角形と比(2 時間) D 本時1/2 〈目標〉 相似な図形に着目しながら,三角形と比についての性質を 理解し,比の性質 を使って長さ求め ることができ。 問題 E/BCのとき xの値を求めなさい。 〇相似な図形に着目し,な




中学3年数学練習問題 図形と相似 平行線と線分の比の問題




平行線と線分の比の定理 の問題の解き方 数学fun
平行線 平行線と線分の比:三角形 問題1 正解1 解説1 問題2 正解2 解説2 平行線と線分の比:台形 線分XEと線分DGは平行 じゃから、平行と線分比の関係から、 AX XD = AE EG が言えるわけじゃな 同じものじゃが、分数の形で書いておくと、 mathjax A X X D = A E E G ・・・式(1) となるわけじゃ(これを、式(1)とするかのぉ) 数学おじさん もう1つ、別1 与えられたルールにあてはめる問題 (1) (2) 1数と式・規則性 テキストページ 氏名 2p 3p 3 連立方程式(割合) (1) (2) 2 連立方程式(人数と個数)




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
・下の三角形でDEとBCは平行のとき、 なお、解説の比の計算は省略していますので、計算方法がわからない人は 比例式の問題!解き方のコツは、この合言葉を覚えるだけ!を見てください。 平行線と線分の比の次は3 平行線と線分の比 「平行線に直線が交わるとき、その交点の間の比は等しくなる」ことを次のように 証明した。直線l,m,nが平行であるとき、かっこに当てはまる語をうめよう。 点aを通り、直線a′に平行な直線を引き、それと直線m,nの交点をd,eとした。平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) が平行




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線にはさまれた線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
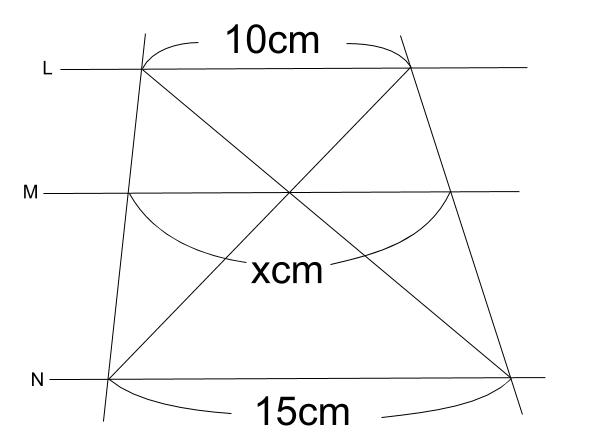
を求めたり,直角三角形 の辺の長さを求めたり するなど,技能を身に付 けている。 相似の意味,三角形の相似 条件,平行線と線分の比に ついての性質,相似比と面 積比及び体積比の関係,円 周角と中心角の関係の意 味などを理解し,知識を身 に付けて2 2 平行線と比 本・平行線と線分の比についての ・三角形と比の性質、中点連結定 時 定理を理解する。 理、平行線と比の性質を、相互に 関連づけてとらえることができる平行線で区切られた線分の比の定理 「平行線と比の定理」の 型と 型は、台形のようなものにも応用できますね! 直線 t を平行移動させた t' も、 当然 a':b' ですね! (t と t' の間の空間は平行四辺形) 実は、3本の平行線(に交わる直線の「 比 」は
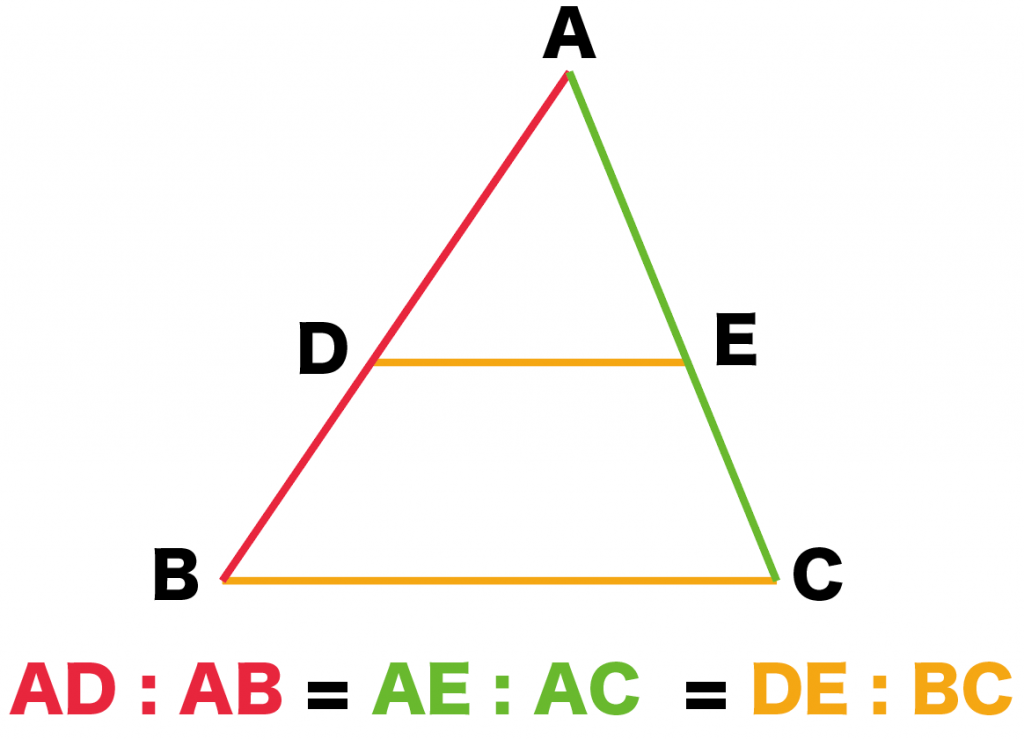



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




中学3年の数学 動画 平行線と線分の比 応用編の問題 19ch
相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 単元 合同な図形と証明,三角形, 「_三角形と線分の比 _平行線と線分の比 pointまとめ. 復習&おさらいにどうぞ🌷」, 学年 中学2年生, キーワード 数学,相似,平行,比,三角形,平行線,中2,図形,幾何,定理,まとめ,math=== 平行線と線分の比 === 三角形の相似条件 次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ.




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube
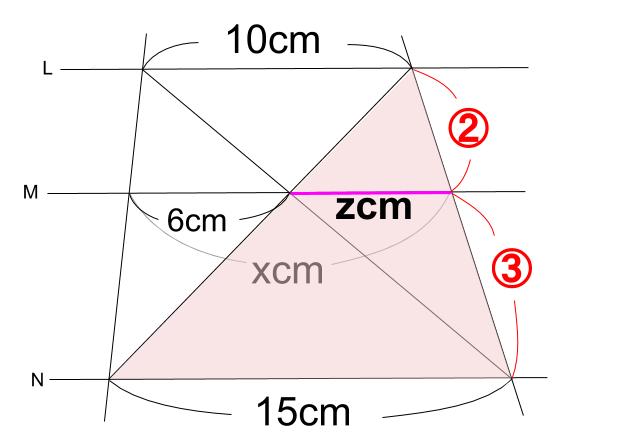



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
平面図形 三角形の性質 三角形の辺と角の大小 例題 練習問題 三角形の3辺の大小関係 例題 練習問題 平行線と線分比 例題 練習問題 線分の内分点と外分点 例題 練習問題 線分の比と三角形の角の二等分線 例題 練習問題 面積と比 例題 練習問題 メネラ平行線と台形中3数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・平行線で三角形を作り、線分の比を利用する 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 326K subscribers平行とは 同一の平面上にあって、 両方向に限りなく延長しても、 いずれの方向においても互いに交わらない直線 ・ (数学的証明) Oから直線lとその平行線mに 垂線 を下す (三角形の内角の和は180°) {∠a =180°−90°−∠O( OaAにおいて) ∠b =180°−90°−∠O( ObB



第5章7 平行線と線分の比 三角形と平行線 フロントエンドなブログ




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
D-10 三角形と平行線 x の値を求めなさい。 ① ③ ② ④ 295 + 76 371 D-11 平行線と線分の比 2つの相似な三角すいで,相似比が2:5だから, 表面積の比は22:52=4:25 平行線が作る2つの三角形は相似になります。 ※相似の問題の解法の応用問題をご参照ください 相似から線分比を使って求めます。 (1)の図形は度々定期試験等で出題されます。・平行線と線分の比・・・5時間 に合った図をかかせ,友だちの図と比べさせた後,QCの長さを実測させた。条件で,三角形の2辺AB,ACの長さしか与えていないので,生徒がかいた ABCは,合同でないものがほとんどである。
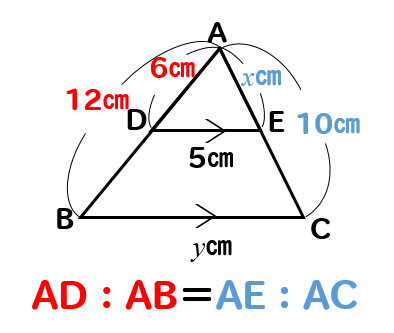



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




数学 中3 49 平行線と線分の比 基本編 Youtube
数学35章図形と相似「平行線と線分の比」<基本問題①・解答> 1 説明※平行線は,三角定規を利用してかく。 ①図のように線分AC上で点Aから 7番目の点と点Bを結ぶ。 ②点Aから5番目の点を通り,①で ひいた線分と平行な線分をひく。FdData 中間期末:中学数学3 年:平行線 三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内
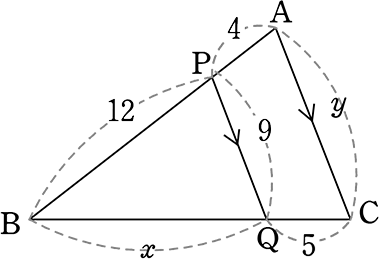



中学数学 図形の相似



Http Www Fdtext Com Dat Suub3 5zukei 2senbunhi Pdf
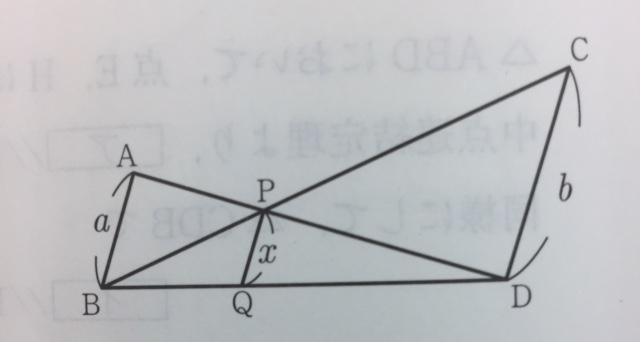



相似 平行線と線分の比 石川県金沢市の個別塾 学習塾 ナビ個別指導学院 泉が丘校ブログ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
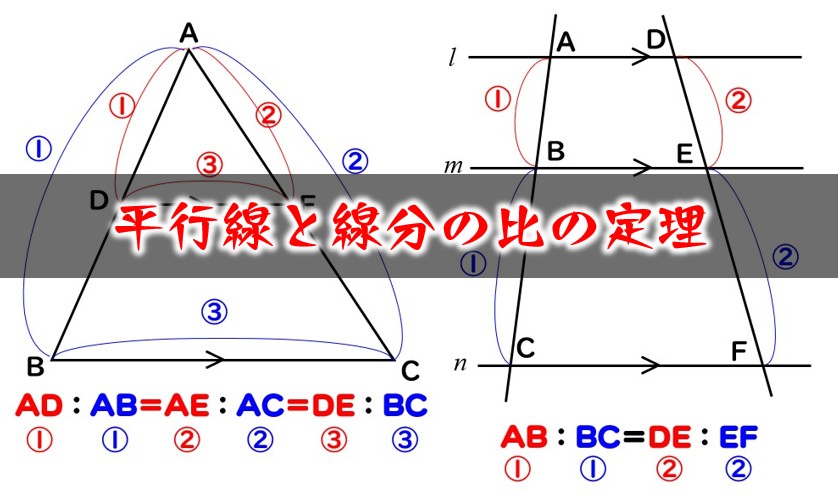



平行線と線分の比の定理 の問題の解き方 数学fun
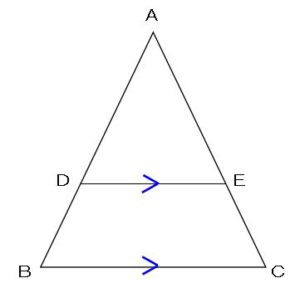



数学 三角形と平行線の線分の比
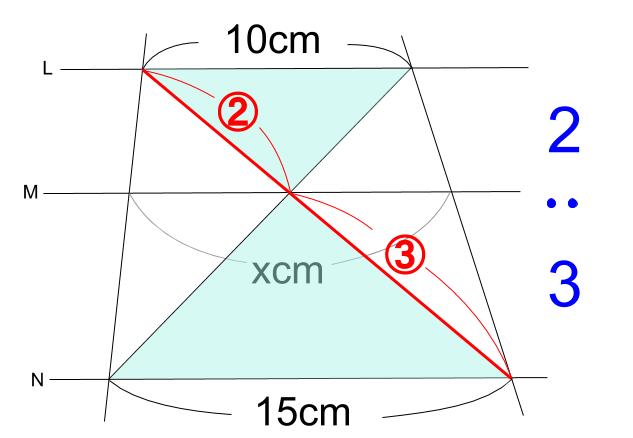



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su
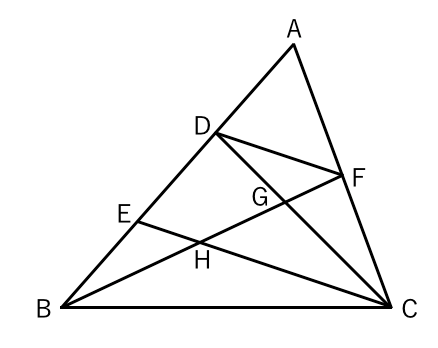



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に
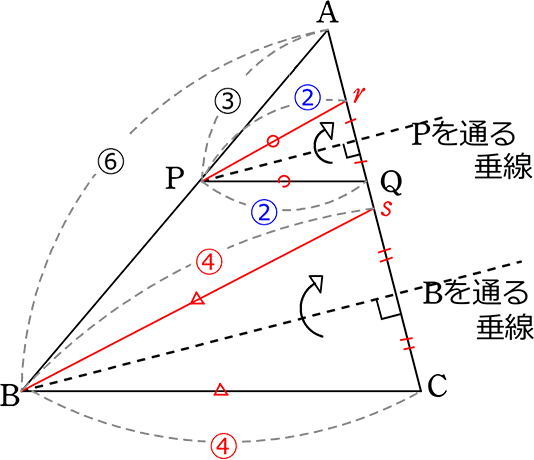



中学数学 図形の相似
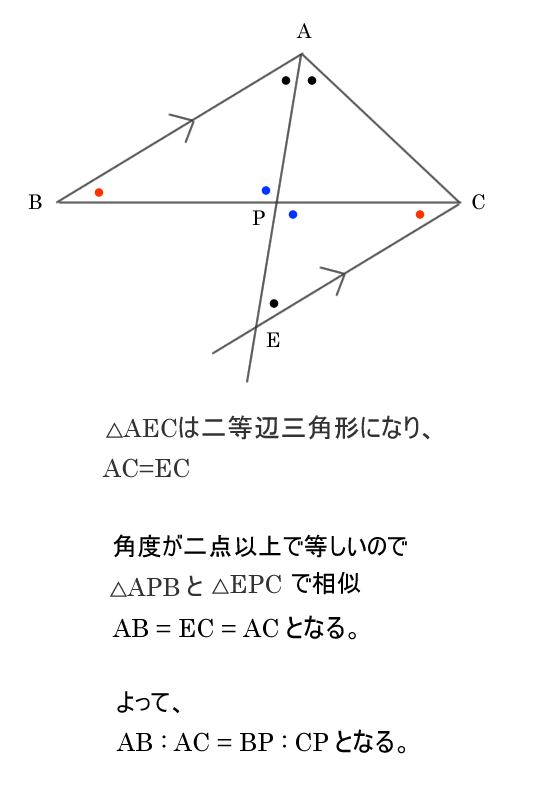



角の二等分線定理 証明 優技録
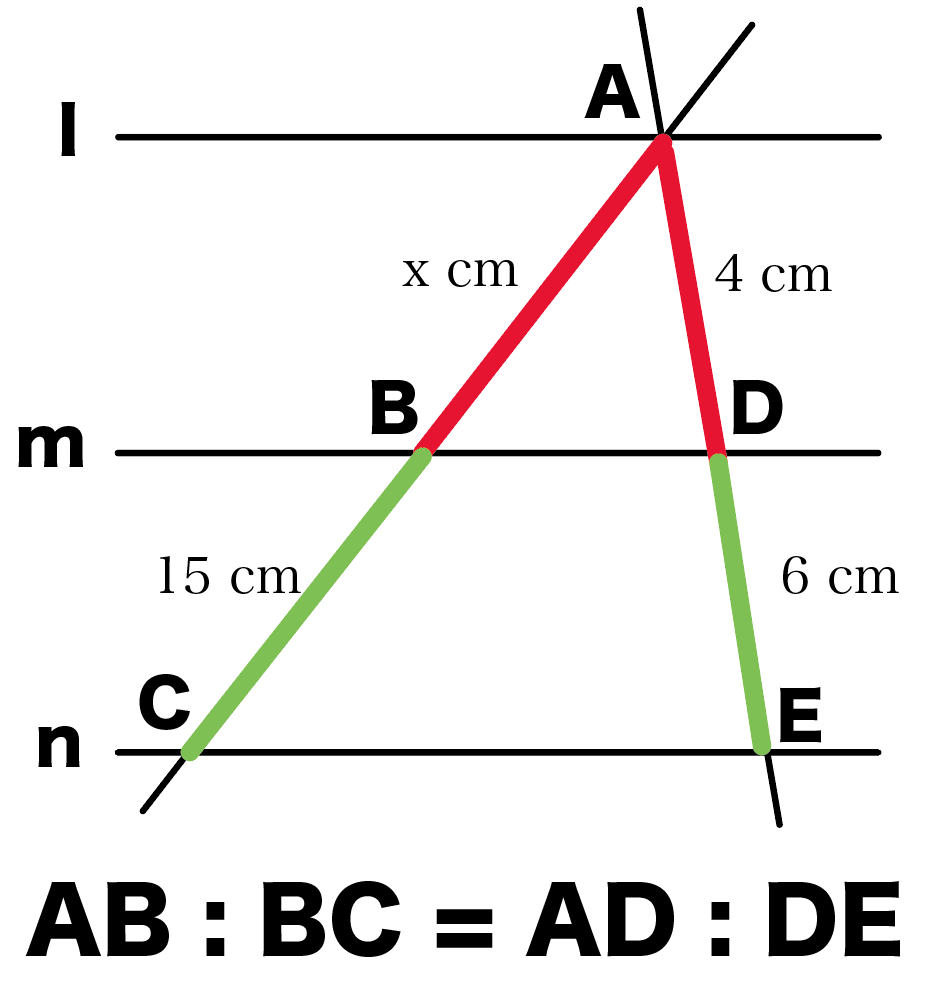



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
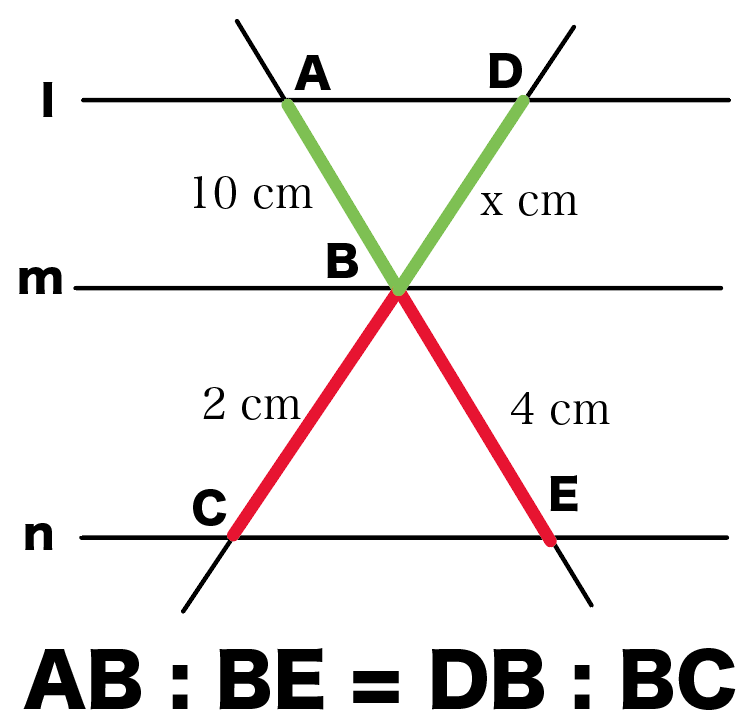



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
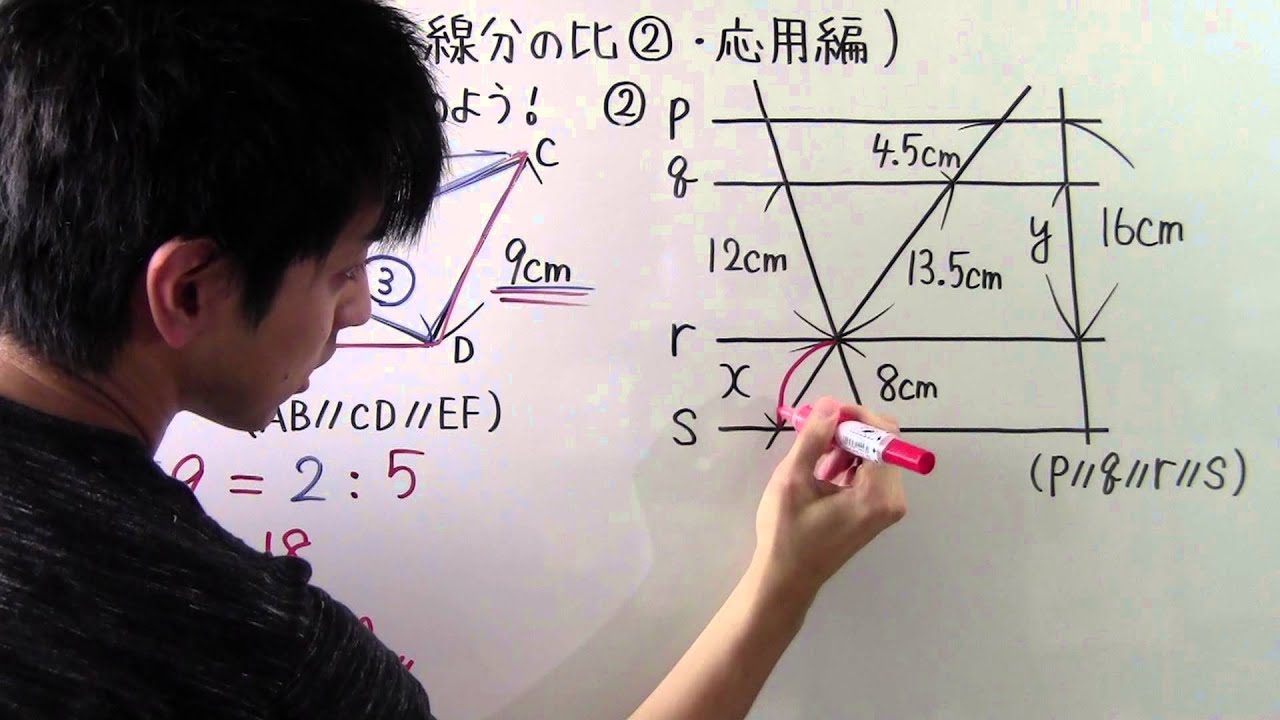



数学 中3 50 平行線と線分の比 応用編 Youtube
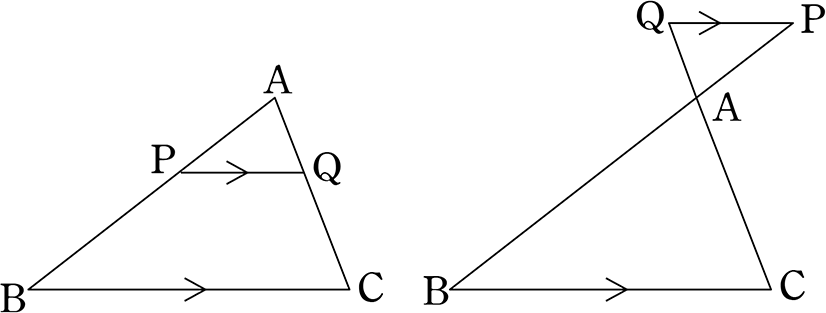



中学数学 図形の相似




中学3年数学練習問題 図形と相似 平行線と線分の比の問題
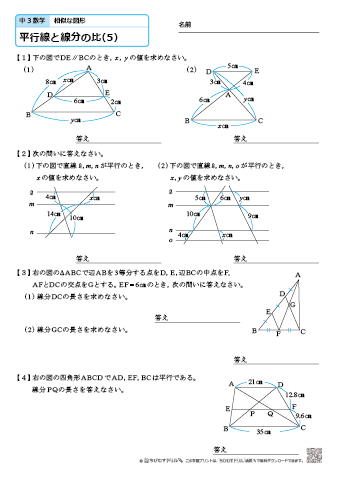



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月
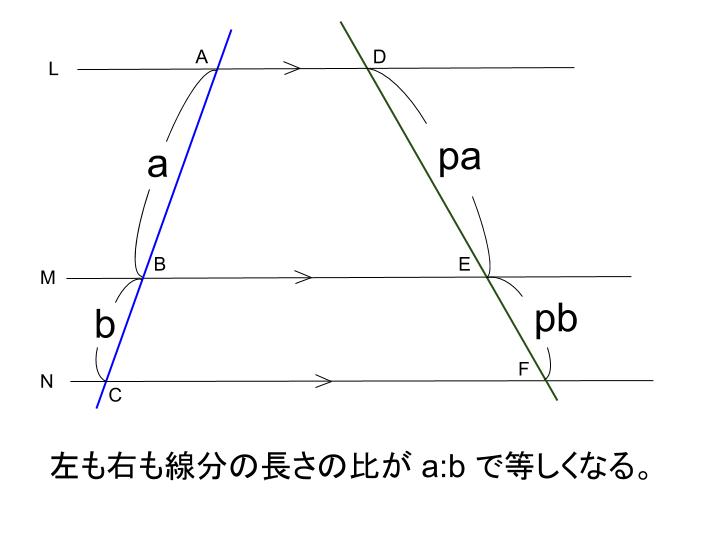



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su
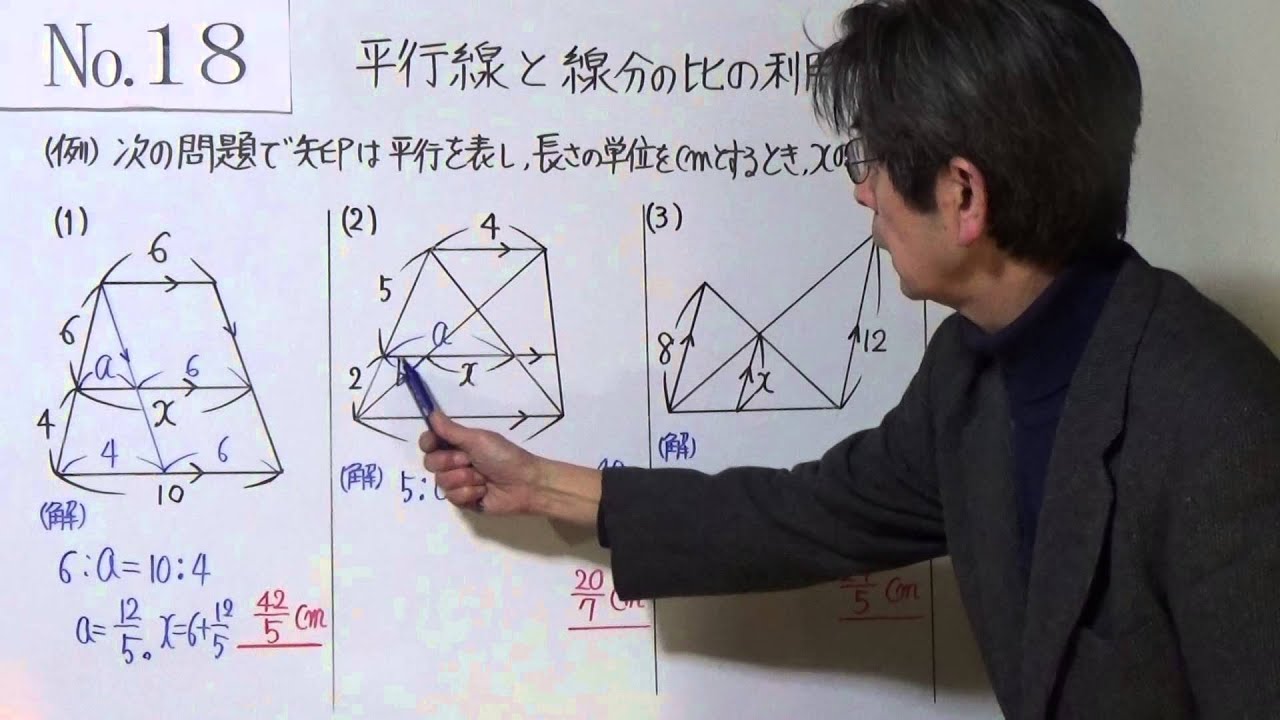



中3 18 5 平行線と線分の比の応用 Youtube



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
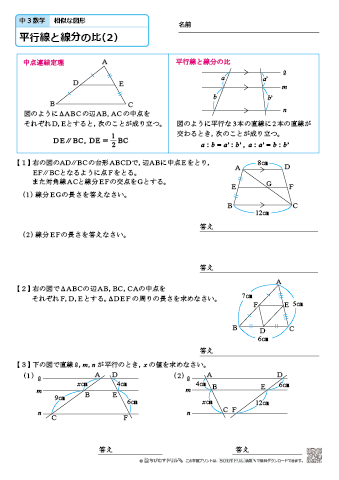



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
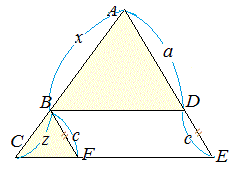



平行線と線分の比




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
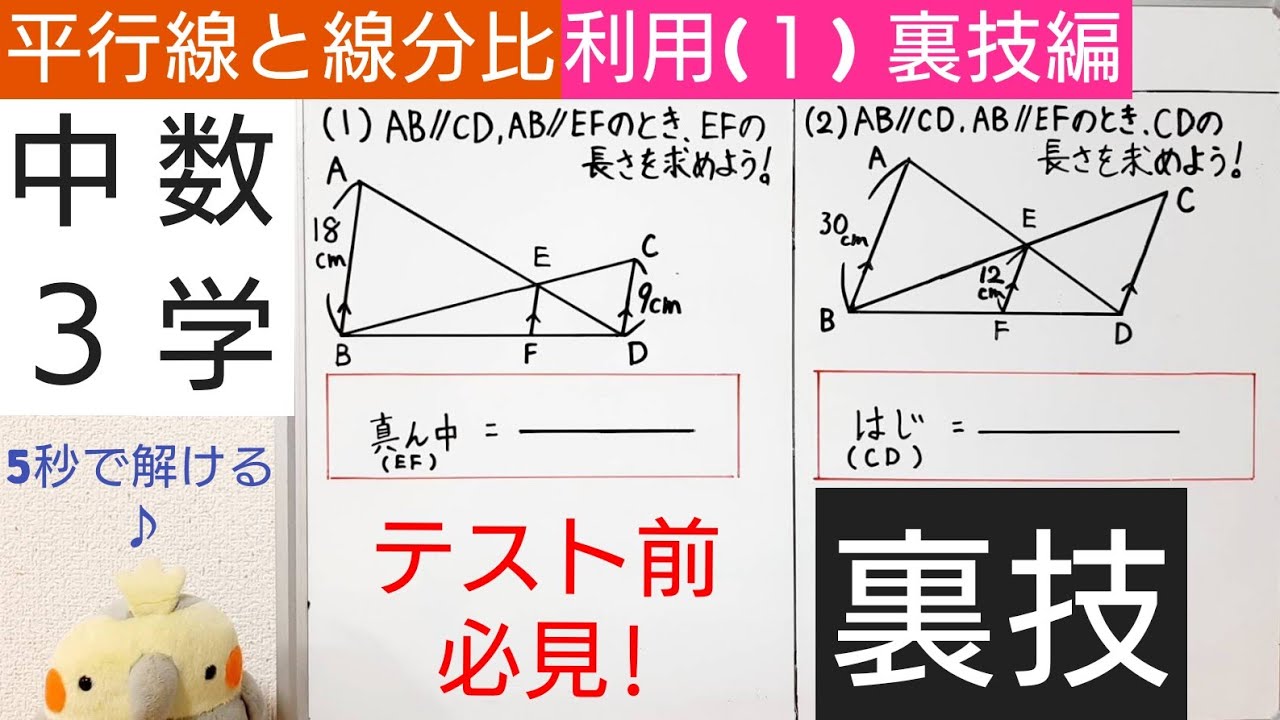



中3数学 15 平行線と線分の比の利用 1 裏技 Youtube



中3数学 平行線と線分比の利用のポイントと練習問題




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
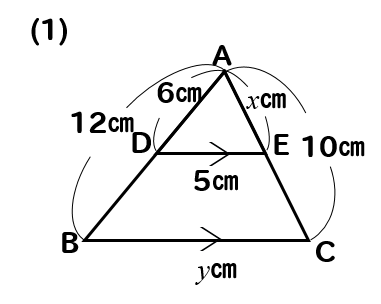



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



高校入試 英語 数学 図形と相似 平行線と線分の比
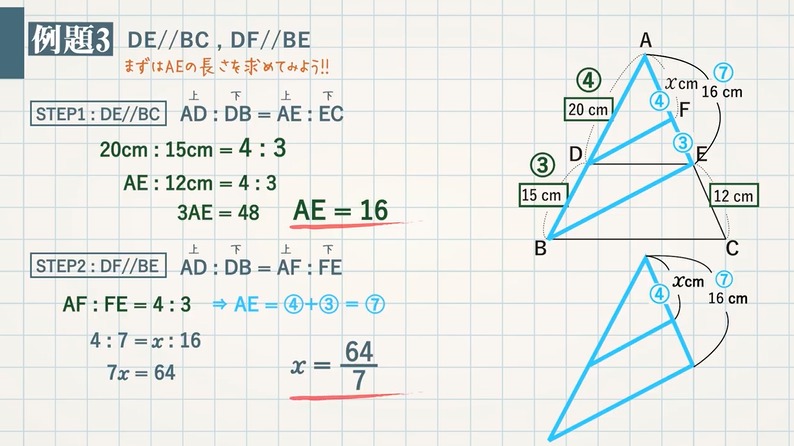



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
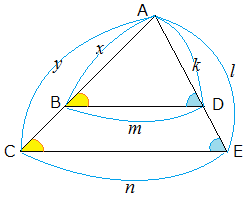



平行線と線分の比
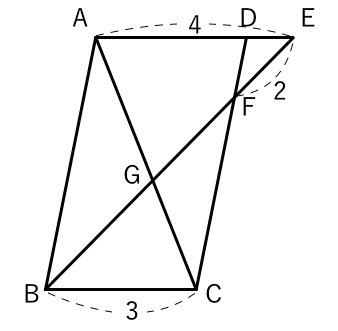



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




中3数学 相似の平行線と線分の比のポイントと定期テスト対策問題
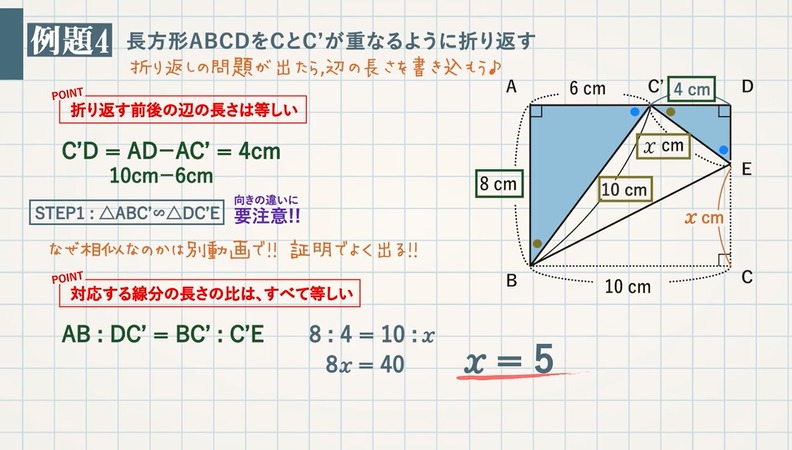



平行線と線分の比 辺の長さを求める応用問題4選 教遊者



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



中学校3年生の数学の授業



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア
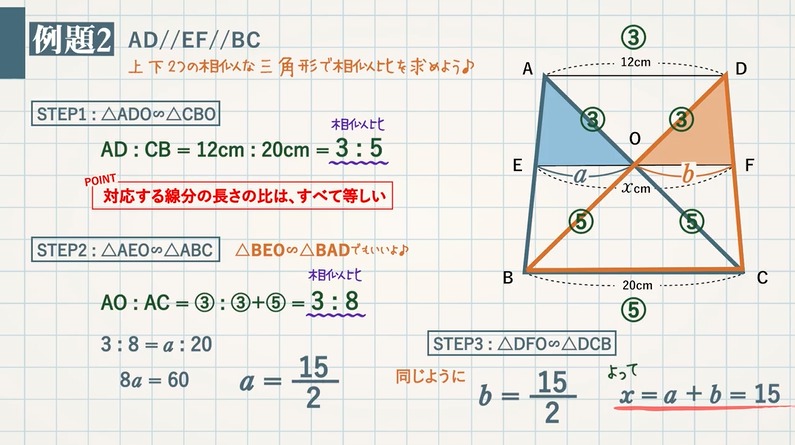



平行線と線分の比 辺の長さを求める応用問題4選 教遊者



1




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張
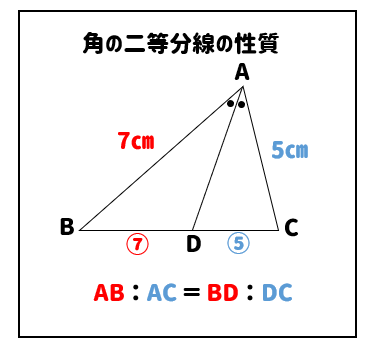



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
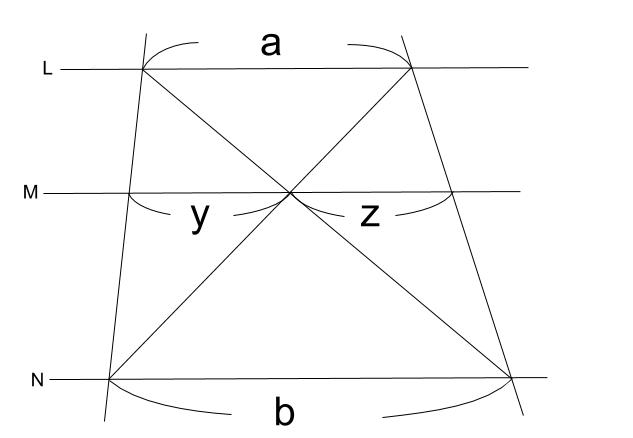



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




中2 相似 平行線と線分の比 中学生 数学のノート Clear




数学 三角形と平行線の線分の比



第5章10 平行線と線分の比 三角形と平行線 中学生




平行線と線分の比 無料で使える中学学習プリント




中3 20 1 線分比と面積比 1 Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
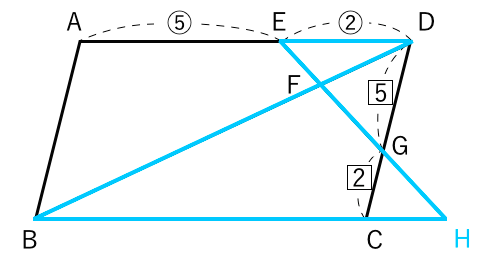



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




平行線と線分の比 Ict教材eboard イーボード




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
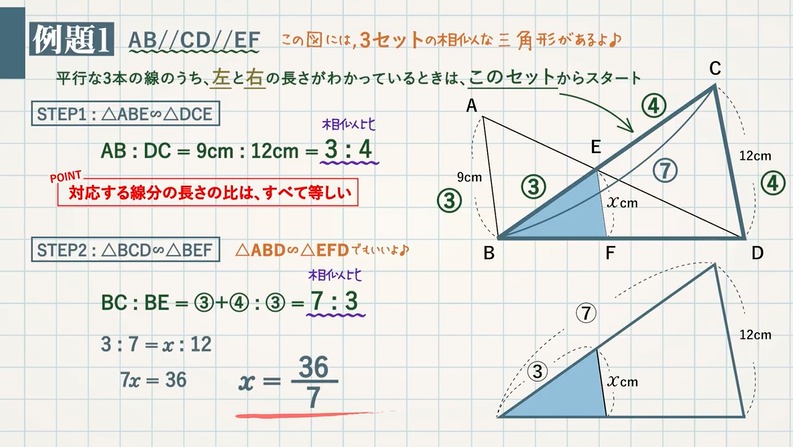



平行線と線分の比 辺の長さを求める応用問題4選 教遊者



平行線と線分の比についてです この図形に平行線と線分の比があるのですが Yahoo 知恵袋




平行線と線分の比 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




平行線と線分の比 の問題を参考に 問題へのアプローチを 現役医師による難関高校受験塾 Core コア




平行線と線分の比の定理 の問題の解き方 数学fun
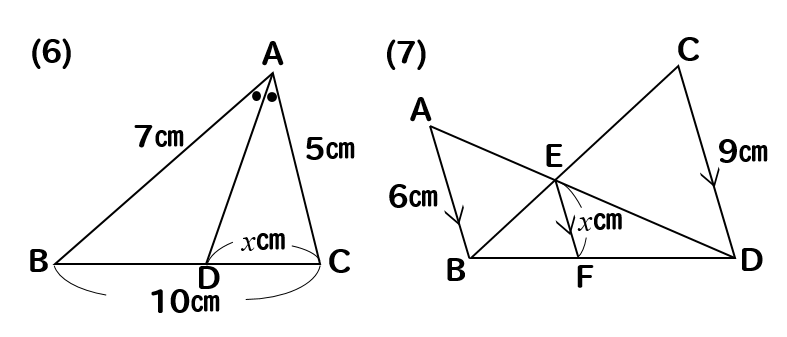



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




平行線と線分の比 三角形の比の取り方を簡単な問題で覚えよう 中学や高校の数学の計算問題
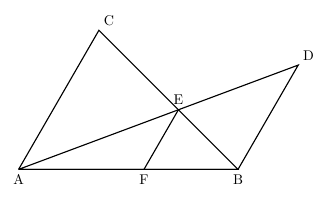



平行線の線分比の問題の解法 夢を叶える塾




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
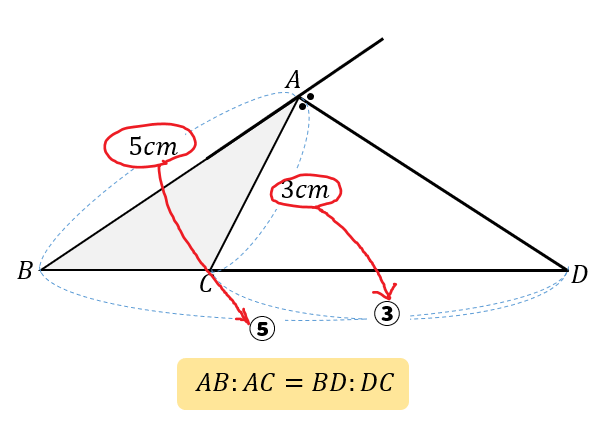



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
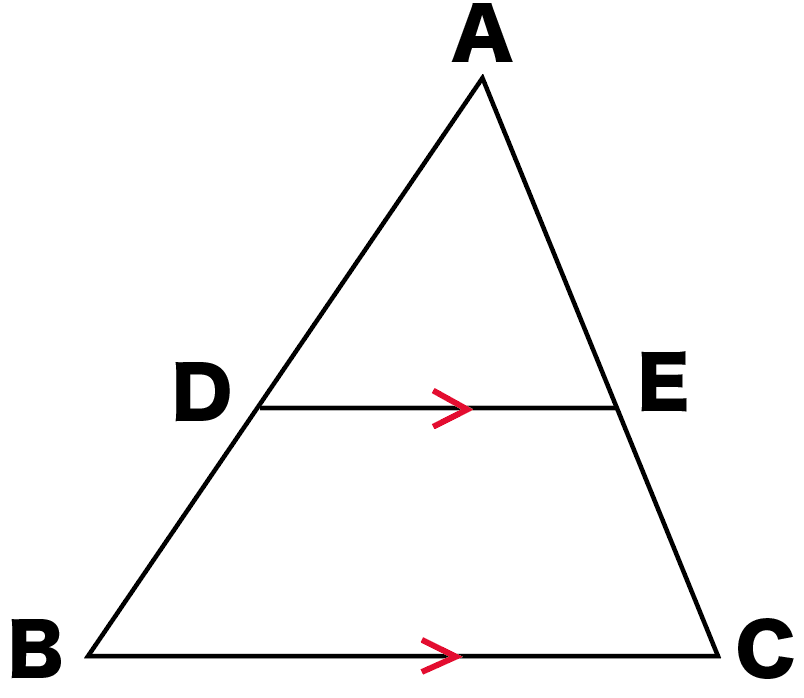



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
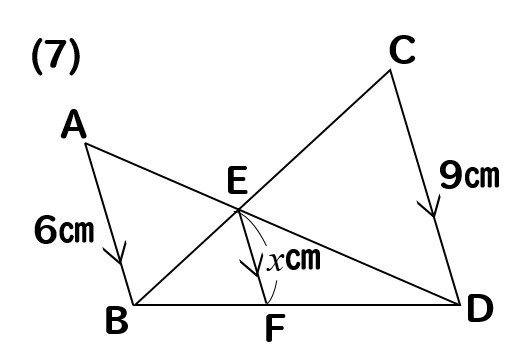



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
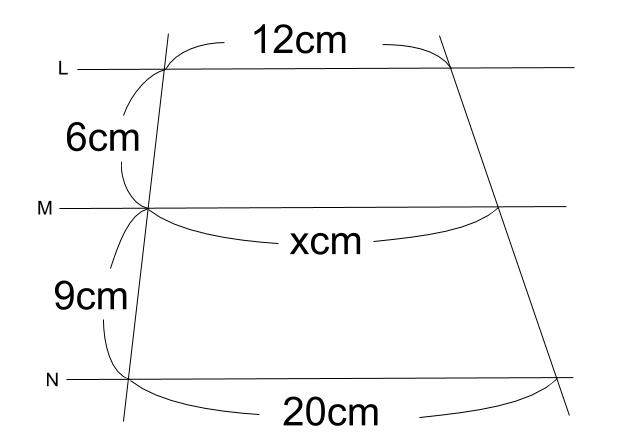



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ



1
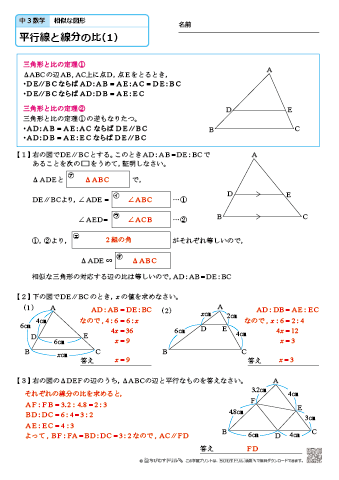



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor平行線と台形 中3数学 Studydoctor
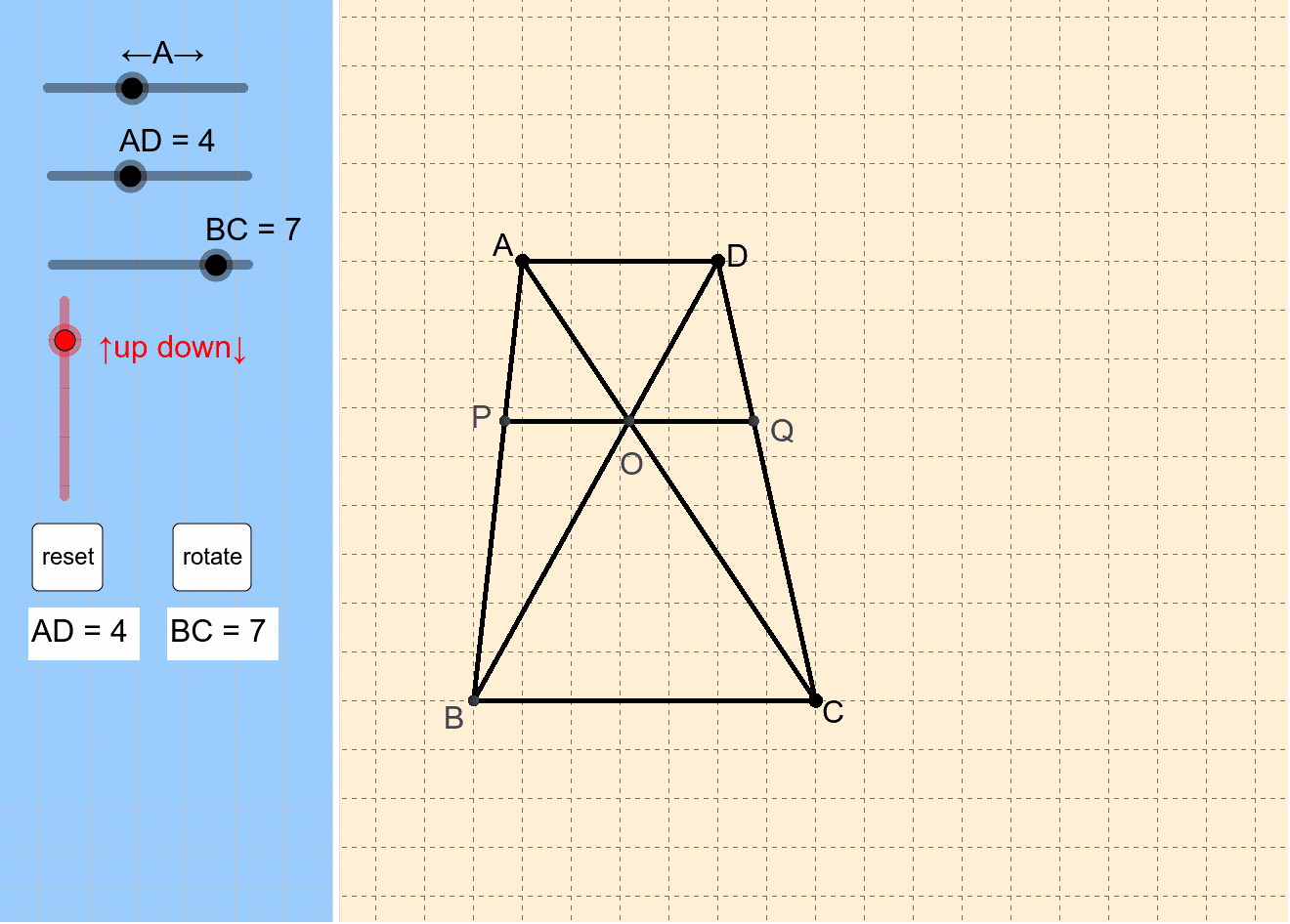



相似 平行線と線分の比 Geogebra
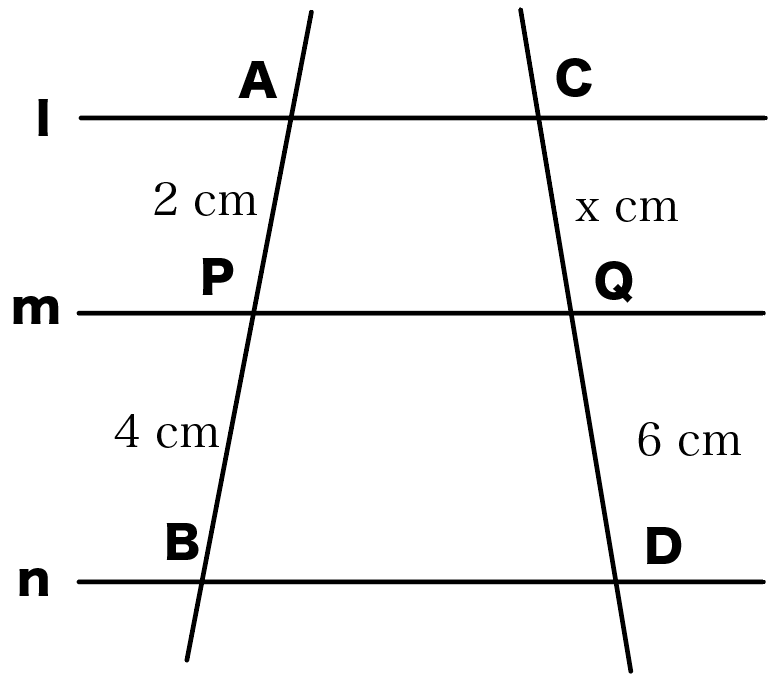



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット
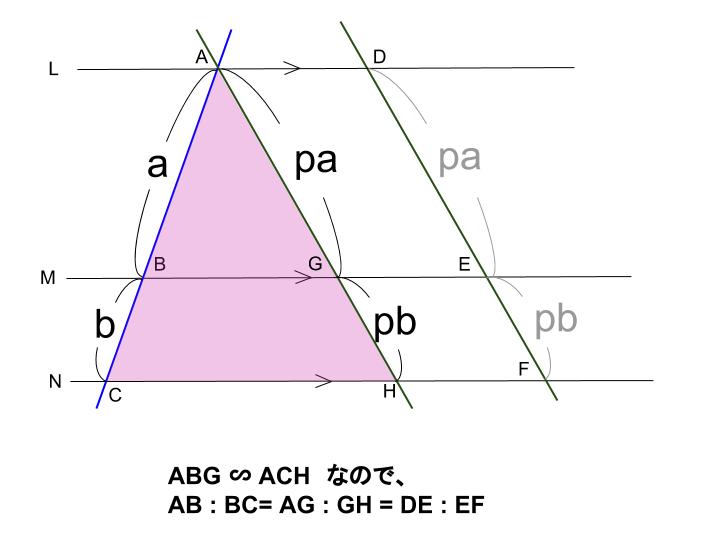



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比の定理 の問題の解き方 数学fun




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




中3数学 相似な図形 平行線と線分の比 違う向きの三角形の場合 Youtube




平行線と線分の比の定理 の問題の解き方 数学fun




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張



1
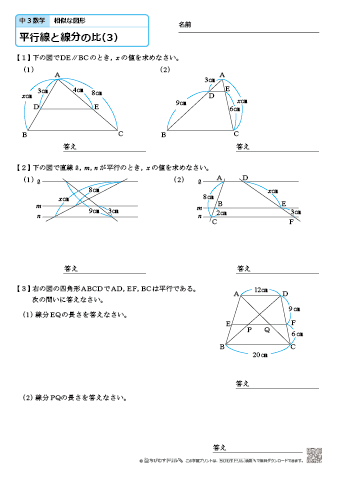



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



0 件のコメント:
コメントを投稿